Когда речь идет о теореме Пифагора, необычное начинается уже с ее названия. Считается, что сформулировал ее впервые отнюдь не Пифагор. Сомнительным полагают и то, что он дал ее доказательство. Если Пифагор - реальное лицо (некоторые сомневаются даже в этом!), то жил он, скорее всего, в VI-V в. до н. э. Сам он ничего не писал, называл себя философом, что значило, в его понимании, «стремящийся к мудрости», основал пифагорейский союз, члены которого занимались музыкой, гимнастикой, математикой, физикой и астрономией. По-видимому, был он и великолепным оратором, о чем свидетельствует следующая легенда, относящаяся к пребыванию его в городе Кротоне: «Первое появление Пифагора пред народом в Кротоне началось речью к юношам, в которой он так строго, но вместе с тем и так увлекательно изложил обязанности юношей, что старейшие в городе просили не оставить и их без поучения. В этой второй речи он указывал на законность и на чистоту нравов, как на основы семейства; в следующих двух он обратился к детям и женщинам. Последствием последней речи, в которой он особенно порицал роскошь, было то, что в храм Геры доставлены были тысячи драгоценных платьев, ибо ни одна женщина не решалась более показываться в них на улице...» Тем не менее еще во втором столетии нашей эры, т. е. спустя 700 лет, жили и творили вполне реальные люди, незаурядные ученые, находившиеся явно под влиянием пифагорейского союза и относящиеся с большим уважением к тому, что согласно легенде создал Пифагор.
Несомненно также, что интерес к теореме вызывается и тем, что она занимает в математике одно из центральных мест, и удовлетворением авторов доказательств, преодолевших трудности, о которых хорошо сказал живший до нашей эры римский поэт Квинт Гораций Флакк: «Трудно хорошо выразить общеизвестные факты».
Первоначально теорема устанавливала соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника:
.
Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b: a 2 +b 2 =c 2 . Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что
a 2 + b 2 = c 2 , существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Доказательства
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).
Через подобные треугольники
Следующее доказательство алгебраической формулировки - наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
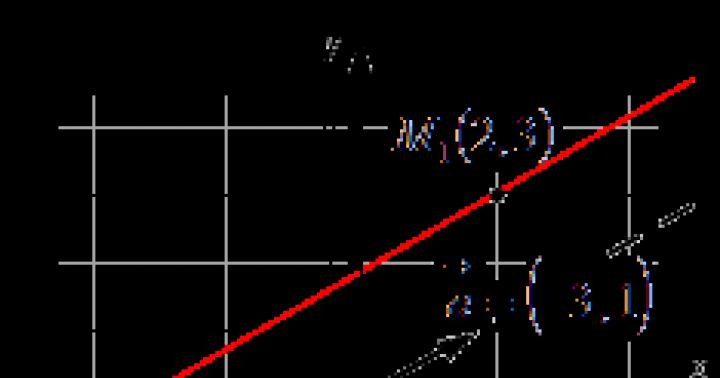
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам.
Аналогично, треугольник CBH подобен ABC. Введя обозначения
получаем
Что эквивалентно
Сложив, получаем
или 
Доказательства методом площадей
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
Доказательство через равнодополняемость
1. Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.2. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол - 180°.
3. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и внутреннего квадрата.
Что и требовалось доказать.
Доказательства через равносоставленность
Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.
Доказательство Евклида
Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.
Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника - BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.
Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, - это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно - AB=AK,AD=AC - равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата - 90°).
Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.
Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах.Доказательство Леонардо да Винчи
Главные элементы доказательства - симметрия и движение.
Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части (так как треугольники ABC и JHI равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки, мы усматриваем равенство заштрихованных фигур CAJI и GDAB. Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна половине площади квадрата, построенного на гипотенузе, плюс площадь исходного треугольника. Последний шаг в доказательстве предоставляется читателю.
Тем, кто интересуется историей теоремы Пифагора, которую изучают в школьной программе, будет также любопытен такой факт, как публикация в 1940 году книги с трехсот семьюдесятью доказательствами этой, казалось бы, простой теоремы. Но она интриговала умы многих математиков и философов разных эпох. В книге рекордов Гиннеса она зафиксирована, как теорема с самым максимальным числом доказательств.
История теоремы Пифагора
Связанная с именем Пифагора, теорема была известна задолго до рождения великого философа. Так, в Египте, при строительстве сооружений, учитывалось соотношение сторон прямоугольного треугольника пять тысячелетий назад. В вавилонских текстах упоминается о все том же соотношении сторон прямоугольного треугольника за 1200 лет до рождения Пифагора.
Возникает вопрос, почему тогда гласит история - возникновение теоремы Пифагора принадлежит ему? Ответ может быть только один - он доказал соотношение сторон в треугольнике. Он сделал то, что века назад не делали те, кто просто пользовался соотношением сторон и гипотенузы, установленным опытным путем.
Из жизни Пифагора
Будущий великий ученый, математик, философ родился на острове Самосе в 570 году до нашей эры. Исторические документы сохранили сведения об отце Пифагора, который был резчиком по драгоценным камням, а вот о матери сведений нет. О родившемся мальчике говорили, что это незаурядный ребенок, проявивший с детского возраста страсть к музыке и поэзии. К учителям юного Пифагора историки относят Гермодаманта и Ферекида Сиросского. Первый ввел мальчика в мир муз, а второй, будучи философом и основателем итальянской школы философии, направил взор юноши к логосу.
В 22 года от роду (548 г. до н. э.) Пифагор отправился в Навкратис для изучения языка и религии египтян. Далее его путь лежал в Мемфис, где благодаря жрецам, пройдя через их хитроумные испытания, он постиг египетскую геометрию, которая, возможно натолкнула пытливого юношу на доказательство теоремы Пифагора. История в дальнейшем припишет теореме именно это имя.
В плену царя Вавилона
По пути домой в Элладу, Пифагор попадает в плен царя Вавилона. Но нахождение в плену принесло пользу пытливому уму начинающего математика, ему было чему поучиться. Ведь в те годы математика в Вавилоне была более развитой чем в Египте. Двенадцать лет он провел за изучением математики, геометрии и магии. И, возможно, именно вавилонская геометрия причастна к доказательству соотношения сторон треугольника и истории открытия теоремы. У Пифагора было для этого достаточно полученных знаний и времени. Но, что это произошло в Вавилоне, документального подтверждения или опровержения тому нет.
В 530 г. до н.э. Пифагор бежит из плена на родину, где живет при дворе тирана Поликрата в статусе полураба. Такая жизнь Пифагора не устраивает, и он удаляется в пещеры Самоса, а затем отправляется на юг Италии, где в то время располагалась греческая колония Кротон.
Тайный монашеский орден
На базе этой колонии Пифагор организовал тайный монашеский орден, представлявший собой религиозный союз и научное общество одновременно. Это общество имело свой устав, в котором говорилось о соблюдении особого образа жизни.
Пифагор утверждал, чтобы понять Бога, человек должен познать такие науки как алгебра и геометрия, знать астрономию и понимать музыку. Исследовательская работа сводилась к познанию мистической стороны чисел и философии. Следует отметить, что проповедованные в то время Пифагором принципы, имеют смысл в подражании и в настоящее время.
Многие из открытий, которые делали ученики Пифагора, приписывались ему. Тем не менее, если говорить кратко, история создания теоремы Пифагора древними историками и биографами того времени, связывается непосредственно с именем этого философа, мыслителя и математика.
Учение Пифагора
Возможно, на мысль о связи теоремы с именем Пифагора натолкнуло историков высказывание великого грека, что в пресловутом треугольнике с его катетами и гипотенузой зашифрованы все явления нашей жизни. А этот треугольник является "ключом" к решению всех возникающих проблем. Великий философ говорил, что следует узреть треугольник, тогда можно считать, что задача на две трети решена.
О своем учении Пифагор рассказывал только своим ученикам устно, не делая никаких записей, держа его в тайне. К великому сожалению, учение величайшего философа не сохранилось до наших дней. Что-то из него просочилось, но нельзя сказать сколько истинного, а сколько ложного в том, что стало известно. Даже с историей теоремы Пифагора не все бесспорно. Историки математики сомневаются в авторстве Пифагора, по их мнению теоремой пользовались за много веков до его рождения.
Теорема Пифагора
Может показаться странным, но исторических фактов доказательства теоремы самим Пифагором нет — ни в архивах, ни в каких-либо других источниках. В современной версии считается, что оно принадлежит не кому иному, как самому Евклиду.
Есть доказательства одного из крупнейших историков математики Морица Кантора, обнаружившего на папирусе, хранящемся в Берлинском музее, записанное египтянами примерно в 2300 году до н. э. равенство, которое гласило: 3² + 4² = 5².
Кратко из истории теоремы Пифагора
Формулировка теоремы из евклидовых "Начал", в переводе звучит также как и в современной интерпретации. Нового в ее прочтении нет: квадрат стороны противолежащей прямому углу, равен сумме квадратов сторон, прилегающих к прямому углу. О том, что теоремой пользовались древние цивилизации Индии и Китая подтверждает трактат "Чжоу — би суань цзинь". Он содержит сведения об египетском треугольнике, в котором описано соотношение сторон как 3:4:5.
Не менее интересна еще одна китайская математическая книга «Чу-пей», в которой также упоминается о пифагоровом треугольнике с пояснением и рисунками, совпадающими с чертежами индусской геометрии Басхары. О самом треугольнике в книге написано, что если прямой угол можно разложить на составные части, тогда линия, которая соединяет концы сторон, будет равна пяти, если основание равно трем, а высота равна четырем.
Индийский трактат "Сульва сутра", относящийся примерно к VII-V векам до н. э., рассказывает о построении прямого угла при помощи египетского треугольника.
Доказательство теоремы
В средние века ученики считали доказательство теоремы слишком трудным делом. Слабые ученики заучивали теоремы наизусть, без понимания смысла доказательства. В связи с этим они получили прозвище "ослы", потому что теорема Пифагора была для них непреодолимым препятствием, как для осла мост. В средние века ученики придумали шутливый стих на предмет этой теоремы.
Чтобы доказать теорему Пифагора самым легким путем, следует просто измерить его стороны, не используя в доказательстве понятие о площадях. Длина стороны, противолежащая прямому углу - это c, а прилежащие к нему a и b, в результате получаем уравнение: a 2 + b 2 = c 2 . Данное утверждение, как говорилось выше, проверяется путем измерения длин сторон прямоугольного треугольника.
Если начать доказательство теоремы с рассмотрения площади прямоугольников, построенных на сторонах треугольника, можно определить площадь всей фигуры. Она будет равна площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырех треугольников и внутреннего квадрата.
(a + b) 2 = 4 x ab/2 + c 2 ;
a 2 + 2ab + b 2 ;
c 2 = a 2 + b 2 , что и требовалось доказать.
Практическое значение теоремы Пифагора заключается в том, что с ее помощью можно найти длины отрезков, не измеряя их. При строительстве сооружений рассчитываются расстояния, размещение опор и балок, определяются центры тяжести. Применяется теорема Пифагора и во всех современных технологиях. Не забыли о теореме и при создании кино в 3D-6D-измерениях, где кроме привычных нам 3-х величин: высоты, длины, ширины - учитываются время, запах и вкус. Как связаны с теоремой вкусы и запахи - спросите вы? Все очень просто - при показе фильма нужно рассчитать, куда и какие запахи и вкусы направлять в зрительном зале.
То ли еще будет. Безграничный простор для открытия и создания новых технологий ждет пытливые умы.
Теорема
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (рис. 1):
$c^{2}=a^{2}+b^{2}$
Доказательство теоремы Пифагора
Пусть треугольник $A B C$ - прямоугольный треугольник с прямым углом $C$ (рис. 2).
Проведём высоту из вершины $C$ на гипотенузу $A B$, основание высоты обозначим как $H$ .
Прямоугольный треугольник $A C H$ подобен треугольнику $A B C$ по двум углам ($\angle A C B=\angle C H A=90^{\circ}$, $\angle A$ - общий). Аналогично, треугольник $C B H$ подобен $A B C$ .
Введя обозначения
$$B C=a, A C=b, A B=c$$
из подобия треугольников получаем, что
$$\frac{a}{c}=\frac{H B}{a}, \frac{b}{c}=\frac{A H}{b}$$
Отсюда имеем, что
$$a^{2}=c \cdot H B, b^{2}=c \cdot A H$$
Сложив полученные равенства, получаем
$$a^{2}+b^{2}=c \cdot H B+c \cdot A H$$
$$a^{2}+b^{2}=c \cdot(H B+A H)$$
$$a^{2}+b^{2}=c \cdot A B$$
$$a^{2}+b^{2}=c \cdot c$$
$$a^{2}+b^{2}=c^{2}$$
Что и требовалось доказать.
Геометрическая формулировка теоремы Пифагора
Теорема
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (рис. 2):
Примеры решения задач
Пример
Задание. Задан прямоугольный треугольник $A B C$, катеты которого равны 6 см и 8 см. Найти гипотенузу этого треугольника.
Решение. Согласно условию катеты $a=6$ см, $b=8$ см. Тогда, согласно теореме Пифагора, квадрат гипотенузы
$c^{2}=a^{2}+b^{2}=6^{2}+8^{2}=36+64=100$
Отсюда получаем, что искомая гипотенуза
$c=\sqrt{100}=10$ (см)
Ответ. 10 см
Пример
Задание. Найти площадь прямоугольного треугольника, если известно, что один из его катетов на 5 см больше другого, а гипотенуза равна 25 см.
Решение. Пусть $x$ см - длина меньшего катета, тогда $(x+5)$ см - длина большего. Тогда согласно теореме Пифагора имеем:
$$x^{2}+(x+5)^{2}=25^{2}$$
Раскрываем скобки, сводим подобные и решаем полученное квадратное уравнение:
$x^{2}+5 x-300=0$
Согласно теореме Виета , получаем, что
$x_{1}=15$ (см) , $x_{2}=-20$ (см)
Значение $x_{2}$ не удовлетворяет условию задачи, а значит, меньший катет равен 15 см, а больший - 20 см.
Площадь прямоугольного треугольника равна полупроизведению длин его катетов, то есть
$$S=\frac{15 \cdot 20}{2}=15 \cdot 10=150\left(\mathrm{см}^{2}\right)$$
Ответ. $S=150\left(\mathrm{см}^{2}\right)$
Историческая справка
Теорема Пифагора - одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
В древнекитайской книге "Чжоу би суань цзин" говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. Крупнейший немецкий историк математики Мориц Кантор (1829 - 1920) считает, что равенство $3^{2}+4^{2}=5^{2}$ было известно уже египтянам ещё около 2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника .
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата , построенного на гипотенузе , равна сумме площадей квадратов ,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c , а длины катетов через a и b :
Обе формулировки теоремы Пифагора эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
измерив только длины сторон прямоугольного треугольника .
Обратная теорема Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
треугольник прямоугольный.
Или, иными словами:
Для всякой тройки положительных чисел a , b и c , такой, что
существует прямоугольный треугольник с катетами a и b и гипотенузой c .
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей , аксиоматические и экзотические доказательства (например,
с помощью дифференциальных уравнений ).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C . Проведём высоту из C и обозначим
её основание через H .
Треугольник ACH подобен треугольнику AB C по двум углам. Аналогично, треугольник CBH подобен ABC .
Введя обозначения:
получаем:
,
что соответствует -
Сложив a 2 и b 2 , получаем:
или , что и требовалось доказать.
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
- Доказательство через равнодополняемость.
Расположим четыре равных прямоугольных
треугольника так, как показано на рисунке
справа.
Четырёхугольник со сторонами c - квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b ), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
наблюдая изменение стороны a , мы можем
записать следующее соотношение для бесконечно
малых приращений сторон с и a (используя подобие
треугольников):
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b ). Тогда для константы интегрирования получим:
Г. Глейзер,
академик РАО, Москва
О теореме Пифагора и способах ее доказательства
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах...
Это одна из самых известных геометрических теорем древности, называемая теоремой Пифагора. Ее и сейчас знают практически все, кто когда-либо изучал планиметрию. Мне кажется, что если мы хотим дать знать внеземным цивилизациям о существовании разумной жизни на Земле, то следует посылать в космос изображение Пифагоровой фигуры. Думаю, что если эту информацию смогут принять мыслящие существа, то они без сложной дешифровки сигнала поймут, что на Земле существует достаточно развитая цивилизация.
Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. С его именем связано много легенд. Достоверно известно, что Пифагор много путешествовал по странам Востока, посещал Египет и Вавилон. В одной из греческих колоний Южной Италии им была основана знаменитая «Пифагорова школа», сыгравшая важную роль в научной и политической жизни древней Греции. Именно Пифагору приписывают доказательство известной геометрической теоремы. На основе преданий, распространенных известными математиками (Прокл, Плутарх и др.), длительное время считали, что до Пифагора эта теорема не была известна, отсюда и название – теорема Пифагора.
Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий. Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении «Чжоу-би», написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам. Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Мы не знаем, как он это сделал. Некоторыми историками математики предполагается, что все же доказательство Пифагора было не принципиальным, а лишь подтверждением, проверкой этого свойства на ряде частных видов треугольников, начиная с равнобедренного прямоугольного треугольника, для которого оно очевидно следует из рис. 1.
С
глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен, но стремление к преумножению их числа сохранилось. Думаю, что самостоятельное «открытие» доказательств теоремы Пифагора будет полезно и современным школьникам.
Рассмотрим некоторые примеры доказательств, которые могут подсказать направления таких поисков.
Доказательство Пифагора
";Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. "; Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для DАВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катететах по два. Теорема доказана.
Доказательства, основанные на использовании понятия равновеликости фигур.
При этом можно рассмотреть доказательства, в которых квадрат, построенный на гипотенузе данного прямоугольного треугольника «складывается» из таких же фигур, что и квадраты, построенные на катетах. Можно рассматривать и такие доказательства, в которых применяется перестановка слагаемых фигур и учитывается ряд новых идей.
На рис. 2 изображено два равных квадрата. Длина сторон каждого квадрата равна a + b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a, b, то останутся равные площади, т. е. c 2 = a 2 + b 2 . Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «смотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.
Аддитивные доказательства.
Эти доказательства основаны на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.
Здесь: ABC – прямоугольный треугольник с прямым углом C; CMN; CKMN; PO||MN; EF||MN.
Самостоятельно докажите попарное равенство треугольников, полученных при разбиении квадратов, построенных на катетах и гипотенузе.
Докажите теорему с помощью этого разбиения.
На основе доказательства ан-Найризия выполнено и другое разложение квадратов на попарно равные фигуры (рис. 5, здесь ABC – прямоугольный треугольник с прямым углом C).
Еще одно доказательство методом разложения квадратов на равные части, называемое «колесом с лопастями», приведено на рис. 6. Здесь: ABC– прямоугольный треугольник с прямым углом C; O – центр квадрата, построенного на большом катете; пунктирные прямые, проходящие через точку O, перпендикулярны или параллельны гипотенузе.
Это разложение квадратов интересно тем, что его попарно равные четырехугольники могут быть отображены друг на друга параллельным переносом. Может быть предложено много и других доказательств теоремы Пифагора с помощью разложения квадратов на фигуры.
Доказательства методом достроения.
Сущность этого метода состоит в том, что к квадратам, построенным на катетах, и к квадрату, построенному на гипотенузе, присоединяют равные фигуры таким образом, чтобы получились равновеликие фигуры.
Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь CEP, прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ.
На рис. 8 Пифагорова фигура достроена до прямоугольника, стороны которого параллельны соответствующим сторонам квадратов, построенных на катетах. Разобьем этот прямоугольник на треугольники и прямоугольники. Из полученного прямоугольника вначале отнимем все многоугольники 1, 2, 3, 4, 5, 6, 7, 8, 9, остался квадрат, построенный на гипотенузе. Затем из того же прямоугольника отнимем прямоугольники 5, 6, 7 и заштрихованные прямоугольники, получим квадраты, построенные на катетах. |
|
|
Теперь докажем, что фигуры, вычитаемые в первом случае, равновелики фигурам, вычитаемым во втором случае.
KLOA = ACPF = ACED = a 2 ;
LGBO = CBMP = CBNQ = b 2 ;
AKGB = AKLO + LGBO = c 2 ;
отсюда c 2 = a 2 + b 2 .
OCLP = ACLF = ACED = b 2 ;
CBML = CBNQ = a 2 ;
OBMP = ABMF = c 2 ;
OBMP = OCLP + CBML;
c 2 = a 2 + b 2 .
Алгебраический метод доказательства.
Рис. 12 иллюстрирует доказательство великого индийского математика Бхаскари (знаменитого автора Лилавати, X |
|
Приведем в современном изложении одно из таких доказательств, принадлежащих Пифагору. |
II в.). Рисунок сопровождало лишь одно слово: СМОТРИ! Среди доказательств теоремы Пифагора алгебраическим методом первое место (возможно, самое древнее) занимает доказательство, использующее подобие.Н
а рис. 13 ABC – прямоугольный, C – прямой угол, CMAB, b 1 – проекция катета b на гипотенузу, a 1 – проекция катета a на гипотенузу, h – высота треугольника, проведенная к гипотенузе.
Из того, что ABC подобен ACM следует
b 2 = cb 1 ; (1)
из того, что ABC подобен BCM следует
a 2 = ca 1 . (2)
Складывая почленно равенства (1) и (2), получим a 2 + b 2 = cb 1 + ca 1 = c(b 1 + a 1) = c 2 .
Если Пифагор действительно предложил такое доказательство, то он был знаком и с целым рядом важных геометрических теорем, которые современные историки математики обычно приписывают Евклиду.
Доказательство Мёльманна (рис. 14). |
Площадь данного прямоугольного треугольника, с одной стороны, равна с другой, где p – полупериметр треугольника, r – радиус вписанной в него окружности 
Имеем:откуда следует, что c 2 =a 2 +b 2 .
во втором 
Приравнивая эти выражения, получаем теорему Пифагора.
Комбинированный метод
Равенство треугольников
c 2 = a 2 + b 2 . (3)
Сравнивая соотношения (3) и (4), получаем, что
c 1 2 = c 2 , или c 1 = c.
Таким образом, треугольники – данный и построенный – равны, так как имеют по три соответственно равные стороны. Угол C 1 прямой, поэтому и угол C данного треугольника тоже прямой.
Древнеиндийское доказательство.
Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика ХП в. Бха-скары помещен чертеж (рис. 4)
характерным для индийских доказательств l словом «смотри!». Как видим, прямоугольнь-ные треугольники уложены здесь гипотенузой наружу и квадрат с 2 перекладывается в «кресло невесты» с 2 -Ь 2 . Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше рис.4 площади данного квадрата) встречаются в древнеиндийском трактате ";Сульва";
Решили прямоугольный треугольник и квадраты, построенные на его катетах, или, иначе, фигуры, составленные из 16 одинаковых равнобедренных прямоугольных треугольников и потому укладывающиеся в квадрат. Такова лили. малая толика богатств, скрытых в жемчужине античной математики - теореме Пифагора.
Древнекитайское доказательство.
Математические трактаты Древнего Китая дошли до нас в редакции П в. до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во П в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг.Главное из сохранившихся астрономических сочинений - в книге «Математика» помещен чертеж (рис. 2, а), доказывающий теорему Пифагора. Ключ к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены г) так, что их внешний контур образует Рис- 2 квадрат со стороной а+Ь, а внутренний - квадрат со стороной с, построенный на гипотенузе (рис. 2, б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. 2, в), то ясно, что образовавшаяся пустота, с одной стороны, равна С 2 , а с другой - с 2 +Ь 2 , т.е. c 2= 2 +b 2 . Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис. 2, а), не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (рис. 2, б) отрезать и приложить гипотенузами к двум другим гипотенузам (рис. 2, г), то легко обнаружить, что
Полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и Ь, т.е. c 2 == a 2 +Ь 2 .
Н
а рисунке 3 воспроизведен чертеж из трактата «Чжоу-би...». Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете-16. Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете.
