1. Строение газообразных, жидких и твердых тел
Молекулярно-кинетическая теория дает возможность понять, почему вещество может находиться в газообразном, жидком и твердом состояниях.
Газы.
В газах расстояние между атомами или молекулами в среднем во много раз больше размеров самих молекул (рис.8.5
). Например, при атмосферном давлении объем сосуда в десятки тысяч раз превышает объем находящихся в нем молекул.
Газы легко сжимаются, при этом уменьшается среднее расстояние между молекулами, но форма молекулы не изменяется (рис.8.6 ).

Молекулы с огромными скоростями - сотни метров в секунду - движутся в пространстве. Сталкиваясь, они отскакивают друг от друга в разные стороны подобно бильярдным шарам. Слабые силы притяжения молекул газа не способны удержать их друг возле друга. Поэтому газы могут нео граниченно расширяться. Они не сохраняют ни формы, ни объема.
Многочисленные удары молекул о стенки сосуда создают давление газа.
Жидкости . Молекулы жидкости расположены почти вплотную друг к другу (рис.8.7 ), поэтому молекула жидкости ведет себя иначе, чем молекула газа. В жидкостях существует так называемый ближний порядок, т. е. упорядоченное расположение молекул сохраняется на расстояниях, равных нескольким молекулярным диаметрам. Молекула колеблется около своего положения равновесия, сталкиваясь с соседними молекулами. Лишь время от времени она совершает очередной «прыжок», попадая в новое положение равновесия. В этом положении равновесия сила отталкивания равна силе притяжения, т. е. суммарная сила взаимодействия молекулы равна нулю. Время оседлой жизни молекулы воды, т. е. время ее колебаний около одного определенного положения равновесия при комнатной температуре, равно в среднем 10 -11 с. Время же одного колебания значительно меньше (10 -12 -10 -13 с). С повышением температуры время оседлой жизни молекул уменьшается.
Характер молекулярного движения в жидкостях, впервые установленный советским физиком Я.И.Френкелем, позволяет понять основные свойства жидкостей.
Молекулы жидкости находятся непосредственно друг возле друга. При уменьшении объема силы отталкивания становятся очень велики. Этим и объясняется малая сжимаемость жидкостей
.
Как известно, жидкости текучи, т. е. не сохраняют своей формы
. Объяснить это можно так. Внешняя сила заметно не меняет числа перескоков молекул в секунду. Но перескоки молекул из одного оседлого положения в другое происходят преимущественно в направлении действия внешней силы (рис.8.8
). Вот почему жидкость течет и принимает форму сосуда.
Твердые тела.
Атомы или молекулы твердых тел, в отличие от атомов и молекул жидкостей, колеблются около определенных положений равновесия. По этой причине твердые тела сохраняют не только объем, но и форму
. Потенциальная энергия взаимодействия молекул твердого тела существенно больше их кинетической энергии.
Есть еще одно важное различие между жидкостями и твердыми телами. Жидкость можно сравнить с толпой людей, где отдельные индивидуумы беспокойно толкутся на месте, а твердое тело подобно стройной когорте тех же индивидуумов, которые хотя и не стоят по стойке смирно, но выдерживают между собой в среднем определенные расстояния. Если соединить центры положений равновесия атомов или ионов твердого тела, то получится правильная пространственная решетка, называемая кристаллической
.
На рисунках 8.9 и 8.10 изображены кристаллические решетки поваренной соли и алмаза. Внутренний порядок в расположении атомов кристаллов приводит к правильным внешним геометрическим формам.


На рисунке 8.11 показаны якутские алмазы.
У газа расстояние l между молекулами много больше размеров молекулr 0:"l>>r 0 .
У жидкостей и твердых телl≈r 0 . Молекулы жидкости расположены в беспорядке и время от времени перескакивают из одного оседлого положения в другое.
У кристаллических твердых тел молекулы (или атомы) расположены строго упорядоченно.
2 . Идеальный газ в молекулярно-кинетической теории
Изучение любой области физики всегда начинается с введения некой модели, в рамках которой идет изучение в дальнейшем. Например, когда мы изучали кинематику, моделью тела была материальная точка и т. д. Как вы уже догадались, модель никогда не будет соответствовать реально происходящим процессам, но часто она очень сильно приближается к этому соответствию.
Молекулярная физика, и в частности МКТ, не является исключением. Над проблемой описания модели работали многие учёные, начиная с восемнадцатого века: М. Ломоносов, Д. Джоуль, Р. Клаузиус (Рис. 1). Последний, собственно, и ввёл в 1857 году модель идеального газа. Качественное объяснение основных свойств вещества на основе молекулярно-кинетической теории не является особенно сложным. Однако теория, устанавливающая количественные связи между измеряемыми на опыте величинами (давлением, температурой и др.) и свойствами самих молекул, их числом и скоростью движения, весьма сложна. У газа при обычных давлениях расстояние между молекулами во много раз превышает их размеры. В этом случае силы взаимодействия молекул пренебрежимо малы и кинетическая энергия молекул много больше потенциальной энергии взаимодействия. Молекулы газа можно рассматривать как материальные точки или очень маленькие твердые шарики. Вместо реального газа , между молекулами которого действуют сложные силы взаимодействия, мы будем рассматривать его модель – идеальный газ.
Идеальный газ – модель газа, в рамках которого молекулы и атомы газа представлены в виде очень маленьких (исчезающих размеров) упругих шариков, которые не взаимодействуют друг с другом (без непосредственного контакта), а только сталкиваются (см. Рис. 2).
Следует отметить, что разреженный водород (под очень маленьким давлением) практически полностью удовлетворяет модели идеального газа.
 Рис. 2.
Рис. 2.
Идеальный газ
- это газ, взаимодействие между молекулами которого пренебрежимо мало. Естественно, при столкновении молекул идеального газа на них действует сила отталкивания. Так как молекулы газа мы можем согласно модели считать материальными точками, то размерами молекул мы пренебрегаем, считая, что объем, который они занимают, гораздо меньше объема сосуда.
Напомним, что в физической модели принимают во внимание лишь те свойства реальной системы, учет которых совершенно необходим для объяснения исследуемых закономерностей поведения этой системы. Ни одна модель не может передать все свойства системы. Сейчас нам предстоит решить довольно узкую задачу: вычислить с помощью молекулярно-кинетической теории давление идеального газа на стенки сосуда. Для этой задачи модель идеального газа оказывается вполне удовлетворительной. Она приводит к результатам, которые подтверждаются опытом.
3. Давление газа в молекулярно-кинетической теории
Пусть газ находится в закрытом сосуде. Манометр показывает давление газа p 0
. Как возникает это давление?
Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с некоторой силой. В результате беспорядочных ударов о стенку давление быстро меняется со временем примерно так, как показано на рисунке 8.12. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади поверхности его чувствительного элемента - мембраны. Несмотря на небольшие изменения давления, среднее значение давления p 0
практически оказывается вполне определенной величиной, так как ударов о стенку очень много, а массы молекул очень малы.

Идеальный газ - модель реального газа. Согласно этой модели молекулы газа можно рассматривать как материальные точки, взаимодействие которых происходит только при их столкновении. Сталкиваясь со стенкой, молекулы газа оказывают на нее давление.
4. Микро- и макропараметры газа
Теперь можно приступить к описанию параметров идеального газа. Они делятся на две группы:
Параметры идеального газа
 То есть микропараметры описывают состояние отдельно взятой частицы (микротела), а макропараметры – состояние всей порции газа (макротела). Запишем теперь соотношение, связывающее одни параметры с другими, или же основное уравнение МКТ:
То есть микропараметры описывают состояние отдельно взятой частицы (микротела), а макропараметры – состояние всей порции газа (макротела). Запишем теперь соотношение, связывающее одни параметры с другими, или же основное уравнение МКТ:
![]()
Здесь: - средняя скорость движения частиц;
Определение. – концентрация частиц газа – количество частиц, приходящихся на единицу объёма; ; единица измерения – .
5. Среднее значение квадрата скорости молекул
Для вычисления среднего давления надо знать среднюю скорость молекул (точнее, среднее значение квадрата скорости). Это не простой вопрос. Вы привыкли к тому, что скорость имеет каждая частица. Средняя же скорость молекул зависит от движения всех частиц.
Средние значения.
С самого начала нужно отказаться от попыток проследить за движением всех молекул, из которых состоит газ. Их слишком много, и движутся они очень сложно. Нам и не нужно знать, как движется каждая молекула. Мы должны выяснить, к какому результату приводит движение всех молекул газа.
Характер движения всей совокупности молекул газа известен из опыта. Молекулы участвуют в беспорядочном (тепловом) движении. Это означает, что скорость любой молекулы может оказаться как очень большой, так и очень малой. Направление движения молекул беспрестанно меняется при их столкновениях друг с другом.
Скорости отдельных молекул могут быть любыми, однако среднее
значение модуля этих скоростей вполне определенное. Точно так же рост учеников в классе неодинаков, но его среднее значение - определенное число. Чтобы это число найти, надо сложить рост отдельных учеников и разделить эту сумму на число учащихся.
Среднее значение квадрата скорости.
В дальнейшем нам понадобится среднее значение не самой скорости, а квадрата скорости. От этой величины зависит средняя кинетическая энергия молекул. А средняя кинетическая энергия молекул, как мы вскоре убедимся, имеет очень большое значение во всей молекулярно-кинетической теории.
Обозначим модули скоростей отдельных молекул газа через . Среднее значение квадрата скорости определяется следующей формулой:
где N
- число молекул в газе.
Но квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат ОХ, ОY, ОZ
. Поэтому
Средние значения величин можно определить с помощью формул, подобных формуле (8.9). Между средним значением и средними значениями квадратов проекций существует такое же соотношение, как соотношение (8.10):
Действительно, для каждой молекулы справедливо равенство (8.10). Сложив такие равенства для отдельных молекул и разделив обе части полученного уравнения на число молекул N
, мы придем к формуле (8.11).
Внимание! Так как направления трех осей ОХ, ОY
и OZ
вследствие беспорядочного движения молекул равноправны, средние значения квадратов проекций скорости равны друг другу:
Видите, из хаоса выплывает определенная закономерность. Смогли бы вы это сообразить сами?
Учитывая соотношение (8.12), подставим в формулу (8.11) вместо и . Тогда для среднего квадрата проекции скорости получим:
![]()
т. е. средний квадрат проекции скорости равен 1/3 среднего квадрата самой скорости. Множитель 1/3 появляется вследствие трехмерности пространства и соответственно существования трех проекций у любого вектора.
Скорости молекул беспорядочно меняются, но средний квадрат скорости вполне определенная величина.
6. Основное уравнение молекулярно-кинетической теории
Приступаем к выводу основного уравнения молекулярно-кинетической теории газов. В этом уравнении устанавливается зависимость давления газа от средней кинетической энергии его молекул. После вывода этого уравнения в XIX в. и экспериментального доказательства его справедливости началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.
Доказательство почти любого утверждения в физике, вывод любого уравнения могут быть проделаны с различной степенью строгости и убедительности: очень упрощенно, более или менее строго или же с полной строгостью, доступной современной науке.
Строгий вывод уравнения молекулярно-кинетической теории газов довольно сложен. Поэтому мы ограничимся сильно упрощенным, схематичным выводом уравнения. Несмотря на все упрощения, результат получится верный.
Вывод основного уравнения.
Вычислим давление газа на стенку CD
сосуда ABCD
площадью S
, перпендикулярную координатной оси OX
(рис.8.13
).
При ударе молекулы о стенку ее импульс изменяется: . Так как модуль скорости молекул при ударе не меняется, то ![]() . Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен .
. Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на нее силы со стороны стенки сосуда, а согласно третьему закону Ньютона таков же по модулю импульс силы, с которой молекула подействовала на стенку. Следовательно, в результате удара молекулы на стенку подействовала сила, импульс которой равен .
Чему равно среднее расстояние между молекулами насыщенного водяного пара при температуре 100° C?
Задача №4.1.65 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t=100^\circ\) C, \(l-?\)
Решение задачи:
Рассмотрим водяной пар в некотором произвольном количестве, равном \(\nu\) моль. Чтобы определить объем \(V\), занимаемый данным количеством водяного пара, нужно воспользоваться уравнением Клапейрона-Менделеева:
В этой формуле \(R\) — универсальная газовая постоянная, равная 8,31 Дж/(моль·К). Давление насыщенного водяного пара \(p\) при температуре 100° C равно 100 кПа, это известный факт, и его должен знать каждый учащийся.
Чтобы определить количество молекул водяного пара \(N\), воспользуемся следующей формулой:
Здесь \(N_А\) — число Авогадро, равное 6,023·10 23 1/моль.
Тогда на каждую молекулу приходится куб объема \(V_0\), очевидно определяемый по формуле:
\[{V_0} = \frac{V}{N}\]
\[{V_0} = \frac{{\nu RT}}{{p\nu {N_А}}} = \frac{{RT}}{{p{N_А}}}\]
Теперь посмотрите на схему к задаче. Каждая молекула условно находится в своем кубе, расстояние между двумя молекулами может меняться от 0 до \(2d\), где \(d\) — длина ребра куба. Среднее же расстояние \(l\) будет равно длине ребра куба \(d\):
Длину ребра \(d\) можно найти так:
В итоге получим такую формулу:
Переведем температуру в шкалу Кельвина и посчитаем ответ:
Ответ: 3,72 нм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Молекулы очень малы, обычные молекулы невозможно рассмотреть даже в самый сильный оптический микроскоп – но некоторые параметры молекул можно довольно точно посчитать (масса), а некоторые получится только очень грубо оценить (размеры, скорость), да еще хорошо бы понять, что такое «размер молекулы» и про какую именно «скорость молекулы» мы говорим. Итак, масса молекулы находится как «масса одного моля»/«число молекул в моле». Например, для молекулы воды m = 0,018/6·1023 = 3·10-26 кг (можно и поточнее посчитать – число Авогадро известно с хорошей точностью, да и молярную массу любой молекулы несложно найти).
Оценка размера молекулы начинается с вопроса о том, что же считать ее размером. Вот если бы она была идеально отполированным кубиком! Однако, она и не кубик, и не шарик и вообще у нее нет четко очерченных границ. Как быть в таких случаях? Начнем издали. Оценим размер куда более знакомого объекта – школьника. Школьников все мы видели, массу среднего школьника примем равной 60 кг (а потом посмотрим – сильно ли влияет этот выбор на результат), плотность школьника – примерно как у воды (вспомним, что стоит как следует вдохнуть воздух, и после этого можно «висеть» в воде, погрузившись почти полностью, а если выдохнуть, то сразу начинаешь тонуть). Теперь можно найти объем школьника: V = 60/1000 = 0,06 куб. метра. Если теперь принять, что школьник имеет форму куба, то его размер находится как корень кубический из объема, т.е. примерно 0,4 м. Вот такой получился размер – меньше роста (размера «в высоту»), больше толщины (размера «в глубину»). Если мы ничего о форме тела школьника не знаем, то лучше этого ответа мы ничего и не найдем (вместо кубика можно было взять шарик, но ответ получился бы примерно тем же, а считать диаметр шара сложнее, чем ребро куба). А вот если у нас есть дополнительная информация (из анализа фотографий, например), то ответ можно сделать куда более разумным. Пусть стало известно, что «ширина» школьника в среднем вчетверо меньше его высоты, а его «глубина» - еще в три раза меньше. Тогда Н*Н/4*Н/12 = V, отсюда Н = 1,5 м (нет смысла делать более точный расчет такой плохо определенной величины, ориентироваться на возможности калькулятора в таком «расчете» просто неграмотно!). Мы получили вполне разумную оценку роста школьника, если бы мы взяли массу порядка 100 кг (и такие школьники бывают!), получим примерно 1,7 – 1,8 м – тоже вполне разумно.
Оценим теперь размер молекулы воды. Найдем объем, который приходится на одну молекулу в «жидкой воде» - в ней молекулы плотнее всего упакованы (сильнее прижаты друг к другу, чем в твердом, «ледяном» состоянии). Моль воды имеет массу 18 г, его объем 18 куб. сантиметров. Тогда на одну молекулу приходится объем V= 18·10-6/6·1023 = 3·10-29 м3. Если у нас нет информации о форме молекулы воды (или – если мы не хотим учитывать сложную форму молекул), проще всего считать ее кубиком и размер найти точно так, как мы только что находили размер кубического школьника: d= (V)1/3 = 3·10-10 м. Вот и все! Оценить влияние формы достаточно сложных молекул на результат расчета можно, например, так: посчитать размер молекул бензина, считая молекулы кубиками – а после этого провести эксперимент, посмотрев площадь пятна от капли бензина на поверхности воды. Считая пленку «жидкой поверхностью толщиной в одну молекулу» и зная массу капли, можно сравнить размеры, полученные этими двумя способами. Очень поучительный получится результат!
Использованная идея годится и для совсем другого расчета. Оценим среднее расстояние между соседними молекулами разреженного газа для конкретного случая - азот при давлении 1 атм и температуре 300К. Для этого найдем объем, который в этом газе приходится на одну молекулу, а дальше все получится просто. Итак, возьмем моль азота при этих условиях и найдем объем указанной в условии порции, а затем разделим этот объем на число молекул: V= R·T/P·NА= 8,3·300/105·6·1023 = 4·10-26 м3. Будем считать, что объем разделен на плотно упакованные кубические клетки, а каждая молекула «в среднем» сидит в центре своей клетки. Тогда среднее расстояние между соседними (ближайшими) молекулами равно ребру кубической клетки: d = (V)1/3 = 3·10-9 м. Видно, что газ разреженный – при таком соотношении между размерами молекулы и расстоянием между «соседями» сами молекулы занимают довольно малую - примерно 1/1000 часть - объема сосуда. Мы и в этом случае провели расчет очень приближенно - такие не слишком определенные величины, как «среднее расстояние между соседними молекулами» нет смысла считать точнее.
Газовые законы и основы МКТ.
Если газ достаточно разреженный (а это – обычное дело, нам чаще всего приходится иметь дело именно с разреженными газами), то практически любой расчет делается при помощи формулы, связывающей давление Р, объем V, количество газа ν и температуру Т – это знаменитое «уравнение состояния идеального газа» P·V= ν·R·T. Как находить одну из этих величин, если заданы все остальные, это совсем просто и понятно. Но можно сформулировать задачу так, что вопрос будет про какую-нибудь другую величину – например, про плотность газа. Итак, задача: найти плотность азота при температуре 300К и давлении 0,2 атм. Решим ее. Судя по условию газ довольно разреженный (воздух, состоящий на 80% из азота и при существенно большем давлении можно считать разреженным, мы им свободно дышим и легко через него проходим), а если бы это было и не так – других формул у нас все равно нет – используем эту, любимую. В условии не задан объем какой-либо порции газа, зададим его сами. Возьмем 1 кубический метр азота и найдем количество газа в этом объеме. Зная молярную массу азота М= 0,028 кг/моль, найдем массу этой порции – и задача решена. Количество газа ν= P·V/R·T, масса m = ν·М =М·P·V/R·T, отсюда плотность ρ= m/V = М·P/R·T = 0,028·20000/(8,3·300) ≈ 0,2 кг/м3. Выбранный нами объем так и не вошел в ответ, выбирали мы его для конкретности – так проще рассуждать, ведь не обязательно сразу сообразишь, что объем может быть каким угодно, а плотность получится одна и та же. Впрочем, можно и сообразить – «взяв объем, скажем, в пять раз больше, мы увеличим ровно в пять раз количество газа, следовательно, какой бы объем ни взять, плотность получится одна и та же». Можно было просто переписать любимую формулу, подставив в нее выражение для количества газа через массу порции газа и его молярную массу: ν = m/М, тогда сразу выражается отношение m/V = М·P/R·T, а это и есть плотность. Можно было взять моль газа и найти занимаемый им объем, после чего сразу находится плотность, ведь масса моля известна. В общем, чем проще задача, тем больше равноценных и красивых способов ее решать…
Вот еще одна задача, где вопрос может показаться неожиданным: найти разность давлений воздуха на высоте 20 м и на высоте 50 м над уровнем земли. Температура 00С, давление 1 атм. Решение: если мы найдем плотность воздуха ρ при этих условиях, то разность давлений ∆P = ρ·g·∆H. Плотность находим так же, как и в предыдущей задаче, сложность только в том, что воздух – это смесь газов. Считая, что он состоит из 80% азота и 20% кислорода, найдем массу моля смеси: m= 0,8·0,028 + 0,2·0,032 ≈ 0,029 кг. Объем, занимаемый этим молем, V= R·T/P и плотность найдется, как отношение этих двух величин. Дальше все понятно, ответ составит примерно 35 Па.
Плотность газа придется рассчитывать и при нахождении, например, подъемной силы воздушного шара заданного объема, при расчете количества воздуха в баллонах акваланга, необходимого для дыхания под водой в течение известного времени, при расчете количества ишаков, необходимых для перевозки заданного количества паров ртути через пустыню и во многих других случаях.
А вот задача посложнее: на столе шумно кипит электрический чайник, потребляемая мощность составляет 1000 Вт, к.п.д. нагревателя 75% (остальное «уходит» в окружающее пространство). Из носика - площадь «носика» 1 см2 - вылетает струя пара, оценить скорость газа в этой струе. Все необходимые данные взять из таблиц.
Решение. Будем считать, что в чайнике над водой образуется насыщенный пар, тогда из носика вылетает струя насыщенного водяного пара при +1000С. Давление такого пара равно 1 атм, легко найти его плотность. Зная мощность, идущую на испарение Р= 0,75·Р0 = 750 Вт и удельную теплоту парообразования (испарения) r = 2300 кДж/кг, найдем массу пара, образующегося за время τ: m= 0,75Р0·τ/r. Плотность мы знаем, тогда легко найти объем этого количества пара. Остальное уже понятно – представим этот объем в виде столбика с площадью поперечного сечения 1 см2, длина этого столбика, деленная на τ и даст нам скорость вылета (такая длина вылетает за секунду). Итак, скорость вылета струи из носика чайника V = m/(ρ·S·τ) = 0,75P0·τ/(r·ρ·S·τ) = 0,75P0·R·T/(r·P·M·S) = 750·8,3·373/(2,3·106·1·105·0,018·1·10-4) ≈ 5 м/с.
(c) Зильберман А. Р.
Молекулярно-кинетическая теория даёт объяснение тому, что все вещества могут находиться в трёх агрегатных состояниях: в твёрдом, жидком и газообразном. Например, лёд, вода и водяной пар. Часто плазму считают четвёртым состоянием вещества.
Агрегатные состояния вещества (от латинского aggrego – присоединяю, связываю) – состояния одного и того же вещества, переходы между которыми сопровождаются изменением его физических свойств. В этом и заключается изменение агрегатных состояний вещества.
Во всех трёх состояниях молекулы одного и того же вещества ничем не отличаются друг от друга, меняется только их расположение, характер теплового движения и силы межмолекулярного взаимодействия.
Движение молекул в газах
В газах обычно расстояние между молекулами и атомами значительно больше размеров молекул, а силы притяжения очень малы. Поэтому газы не имеют собственной формы и постоянного объёма. Газы легко сжимаются, потому что силы отталкивания на больших расстояниях также малы. Газы обладают свойством неограниченно расширяться, заполняя весь предоставленный им объём. Молекулы газа движутся с очень большими скоростями, сталкиваются между собой, отскакивают друг от друга в разные стороны. Многочисленные удары молекул о стенки сосуда создают давление газа .
Движение молекул в жидкостях
В жидкостях молекулы не только колеблются около положения равновесия, но и совершают перескоки из одного положения равновесия в соседнее. Эти перескоки происходят периодически. Временной отрезок между такими перескоками получил название среднее время оседлой жизни (или среднее время релаксации ) и обозначается буквой?. Иными словами, время релаксации – это время колебаний около одного определённого положения равновесия. При комнатной температуре это время составляет в среднем 10 -11 с. Время одного колебания составляет 10 -12 …10 -13 с.
Время оседлой жизни уменьшается с повышением температуры. Расстояние между молекулами жидкости меньше размеров молекул, частицы расположены близко друг к другу, а межмолекулярное притяжение велико. Тем не менее, расположение молекул жидкости не является строго упорядоченным по всему объёму.
Жидкости, как и твёрдые тела, сохраняют свой объём, но не имеют собственной формы. Поэтому они принимают форму сосуда, в котором находятся. Жидкость обладает таким свойством, как текучесть . Благодаря этому свойству жидкость не сопротивляется изменению формы, мало сжимается, а её физические свойства одинаковы по всем направлениям внутри жидкости (изотропия жидкостей). Впервые характер молекулярного движения в жидкостях установил советский физик Яков Ильич Френкель (1894 – 1952).
Движение молекул в твёрдых телах
Молекулы и атомы твёрдого тела расположены в определённом порядке и образуют кристаллическую решётку . Такие твёрдые вещества называют кристаллическими. Атомы совершают колебательные движения около положения равновесия, а притяжение между ними очень велико. Поэтому твёрдые тела в обычных условиях сохраняют объём и имеют собственную форму.
Физика
![]()
![]()
Взаимодействие между атомами и молекулами вещества. Строение твердых, жидких и газообразных тел
Между молекулами вещества действуют одновременно силы притяжения и силы отталкивания. Эти силы в большой степени зависят от расстояний между молекулами.
Согласно экспериментальным и теоретическим исследованиям межмолекулярные силы взаимодействия обратно пропорциональны n-й степени расстояния между молекулами:
где для сил притяжения n = 7, а для сил отталкивания .
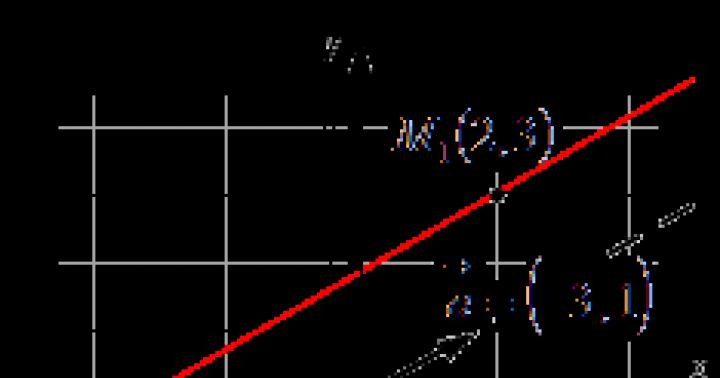
Взаимодействие двух молекул можно описать при помощи графика зависимости проекции равнодействующей сил притяжения и отталкивания молекул от расстояния r между их центрами. Направим ось r от молекулы 1, центр которой совпадает с началом координат, к находящемуся от него на расстоянии центру молекулы 2 (рис. 1).

Тогда проекция силы отталкивания молекулы 2 от молекулы 1 на ось r будет положительной. Проекция силы притяжения молекулы 2 к молекуле 1 будет отрицательной.
Силы отталкивания (рис. 2) гораздо больше сил притяжения на малых расстояниях , но гораздо быстрее убывают с увеличением r. Силы притяжения тоже быстро убывают с увеличением r, так что, начиная с некоторого расстояния , взаимодействием молекул можно пренебречь. Наибольшее расстояние rm, на котором молекулы еще взаимодействуют, называется радиусом молекулярного действия ![]() .
.

Силы отталкивания по модулю равны силам притяжения.
Расстояние соответствует устойчивому равновесному взаимному положению молекул.
В различных агрегатных состояниях вещества расстояние между его молекулами различно. Отсюда и различие в силовом взаимодействии молекул и существенное различие в характере движения молекул газов, жидкостей и твердых тел.
В газах расстояния между молекулами в несколько раз превышают размеры самих молекул. Вследствие этого силы взаимодействия между молекулами газа малы и кинетическая энергия теплового движения молекул намного превышает потенциальную энергию их взаимодействия. Каждая молекула движется свободно от других молекул с огромными скоростями (сотни метров в секунду), меняя направление и модуль скорости при столкновениях с другими молекулами. Длина свободного пробега молекул газа зависит от давления и температуры газа. При нормальных условиях .
В жидкостях расстояние между молекулами значительно меньше, чем в газах. Силы взаимодействия между молекулами велики, и кинетическая энергия движения молекул соизмерима с потенциальной энергией их взаимодействия, вследствие чего молекулы жидкости совершают колебания около некоторого положения равновесия, затем скачкообразно переходят в новые положения равновесия через очень малые промежутки времени , что приводит к текучести жидкости. Таким образом, в жидкости молекулы совершают в основном колебательные и поступательные движения. В твердых телах силы взаимодействия между молекулами настолько велики, что кинетическая энергия движения молекул намного меньше потенциальной энергии их взаимодействия. Молекулы совершают лишь колебания с малой амплитудой около некоторого постоянного положения равновесия - узла кристаллической решетки.
Это расстояние можно оценить, зная плотность вещества и молярную массу . Концентрация – число частиц в единице объема, связана с плотностью, молярной массой и числом Авогадро соотношением.