Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.
Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 (x 1 , y 1) и направляющий вектор заданной прямой a → = (a x , a y) . Дадим описание заданной прямой a , используя уравнения.
Используем произвольную точку М (x , y) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = (x - x 1 , y - y 1) . Опишем полученное: прямая задана множеством точек М (x , y) , проходит через точку М 1 (x 1 , y 1) и имеет направляющий вектор a → = (a x , a y) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = (x - x 1 , y - y 1) и a → = (a x , a y) являются коллинеарными.
Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = (x - x 1 , y - y 1) и a → = (a x , a y) возможно записать в виде уравнения:
M 1 M → = λ · a → , где λ – некоторое действительное число.
Определение 1
Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.
В координатной форме оно имеет вид:
M 1 M → = λ · a → ⇔ x - x 1 = λ · a x y - y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ
Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ
Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 (x 1 , y 1) и имеет направляющий вектор a → = (a x , a y) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.
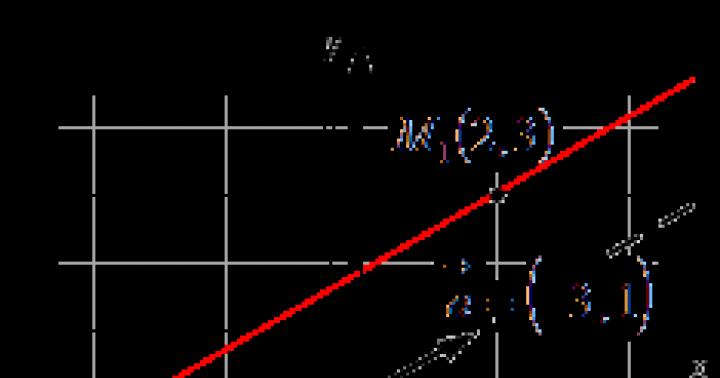
Пример 1
Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 (2 , 3) и ее направляющий вектор a → = (3 , 1) .
Решение
На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ
Наглядно проиллюстрируем:

Ответ: x = 2 + 3 · λ y = 3 + λ
Необходимо отметить: если вектор a → = (a x , a y) служит направляющим вектором прямой а, а точки М 1 (x 1 , y 1) и М 2 (x 2 , y 2) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .
К примеру, нам заданы направляющий вектор прямой a → = (2 , - 1) , а также точки М 1 (1 , - 2) и М 2 (3 , - 3) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = - 2 - λ или x = 3 + 2 · λ y = - 3 - λ .
Следует обратить внимание и на такой факт: если a → = (a x , a y) - направляющий вектор прямой a , то ее направляющим векторомбудет и любой из векторов μ · a → = (μ · a x , μ · a y) , где μ ϵ R , μ ≠ 0 .
Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.
Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = - 2 - 5 · λ . Тогда a → = (2 , - 5) - направляющий векторэтой прямой. А также любой из векторов μ · a → = (μ · 2 , μ · - 5) = 2 μ , - 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор - 2 · a → = (- 4 , 10) , ему соответствует значение μ = - 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 - 4 · λ y = - 2 + 10 · λ .
Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно
В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.
Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x - x 1 a x = y - y 1 a y .
Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y
При этом не должно смущать, если a x или a y будут равны нулю.
Пример 2
Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = - 2 - 4 · λ к каноническому уравнению.
Решение
Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = - 2 - 4 · λ
Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = - 2 - 4 · λ ⇔ λ = x - 3 0 λ = y + 2 - 4
Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:
x - 3 0 = y + 2 - 4
Ответ: x - 3 0 = y + 2 - 4
В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y ⇔ ⇔ a y · (x - x 1) = a x · (y - y 1) ⇔ A x + B y + C = 0
Пример 3
Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = - 1 + 2 · λ y = - 3 · λ
Решение
Для начала осуществим переход к каноническому уравнению:
x = - 1 + 2 · λ y = - 3 · λ ⇔ λ = x + 1 2 λ = y - 3 ⇔ x + 1 2 = y - 3
Полученная пропорция идентична равенству - 3 · (x + 1) = 2 · y . Раскроем скобки и получим общее уравнение прямой: - 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .
Ответ: 3 x + 2 y + 3 = 0
Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.
Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.
Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x - x 1 a x = y - y 1 a y . Каждое из отношений этого равенства примем равным параметру λ:
x - x 1 a x = y - y 1 a y = λ ⇔ λ = x - x 1 a x λ = y - y 1 a y
Разрешим полученные уравнения относительно переменных x и y:
x = x 1 + a x · λ y = y 1 + a y · λ
Пример 4
Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x - 2 5 = y - 2 2
Решение
Приравняем части известного уравнения к параметру λ: x - 2 5 = y - 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x - 2 5 = y - 2 2 = λ ⇔ λ = x - 2 5 λ = y - 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ
Ответ: x = 2 + 5 · λ y = 2 + 2 · λ
Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.
Пример 5
Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x - 3 y - 3 = 0 .
Решение
Заданное общее уравнение преобразуем в уравнение канонического вида:
4 x - 3 y - 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4
Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:
x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = - 1 3 + 4 · λ
Ответ: x = 3 · λ y = - 1 3 + 4 · λ
Примеры и задачи с параметрическими уравнениями прямой на плоскости
Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.
- В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.
Решение таких задач опирается на следующий факт: числа (x , y) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.
Пример 6
Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 - 1 6 · λ y = - 1 + 2 · λ при λ = 3 .
Решение
Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 - 1 6 · 3 y = - 1 + 2 · 3 ⇔ x = 1 1 2 y = 5
Ответ: 1 1 2 , 5
Также возможна следующая задача: пусть задана некоторая точка M 0 (x 0 , y 0) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .
Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.
Пример 7
Заданы точки М 0 (4 , - 2) и N 0 (- 2 , 1) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = - 1 - 1 2 · λ .
Решение
Подставим координаты точки М 0 (4 , - 2) в заданные параметрические уравнения:
4 = 2 · λ - 2 = - 1 - 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2
Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .
2 = 2 · λ 1 = - 1 - 1 2 · λ ⇔ λ = - 1 λ = - 4
Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 (- 2 , 1) .
Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.
- В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.
Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y - 3 - 1 .
Решение
По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y - 3 - 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y - 3 - 1 , который запишем в виде: a → = (2 , - 1) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + (- 1) · λ ⇔ x = 1 2 + x · λ y = 2 3 - λ
Ответ: x = 1 2 + x · λ y = 2 3 - λ .
Пример 9
Задана точка М 1 (0 , - 7) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .
Решение
В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты (3 , - 2) . Запишем требуемые параметрические уравнения прямой:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = - 7 + (- 2) · λ ⇔ x = 3 · λ y = - 7 - 2 · λ
Ответ: x = 3 · λ y = - 7 - 2 · λ
- В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.
Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 - 3 4 · λ y = - 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.
Решение
Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:
x = 1 - 3 4 · λ y = - 1 + λ ⇔ λ = x - 1 - 3 4 λ = y + 1 1 ⇔ x - 1 - 3 4 = y + 1 1 ⇔ ⇔ 1 · x - 1 = - 3 4 · y + 1 ⇔ x + 3 4 y - 1 4 = 0
Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 - 3 4 · λ y = - 1 + λ имеет координаты 1 , 3 4 .
Ответ: 1 , 3 4 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Векторное и параметрические уравнения плоскости. Пусть r 0 и r - радиус-векторы точек М 0 и M соответственно. Тогда M 0 M = r - r 0 , и условие (5.1) принадлежности точки M плоскости, проходящей через точку М 0 перпендикулярно ненулевому вектору n (рис. 5.2, а), можно записать с помощью скалярного произведения в виде соотношения
n(r - r 0) = 0, (5.4)
которое называют векторным уравнением плоскости.
Фиксированной плоскости в пространстве соответствует множество параллельных ей векторов, т.е. пространство V 2 . Выберем в этом пространстве базис e 1 , e 2 , т.е. пару неколлинеарных векторов, параллельных рассматриваемой плоскости, и точку M 0 на плоскости. Если точка M принадлежит плоскости, то это эквивалентно тому, что ей параллелен вектор M 0 M (рис. 5.2, б), т.е. он принадлежит указанному пространству V 2 . Это означает, что существует разложение вектора M 0 M в базисе e 1 , e 2 , т.е. существуют такие числа t 1 и t 2 , для которых M 0 M = t 1 e 1 + t 2 e 2 . Записав левую часть этого уравнения через радиус-векторы r 0 и r точек М 0 и M соответственно, получаем векторное параметрическое уравнение плоскости
r = r 0 + t 1 e 1 + t 2 e 2 , t 1 , t 1 ∈ R. (5.5)
Чтобы перейти от равенства векторов в (5.5) к равенству их координат , обозначим через (x 0 ; y 0 ; z 0), (x; y; z) координаты точек M 0 , M и через {e 1x ; e 1y ; e 1z }, {e 2x ; e 2y ; e 2z } координаты векторов e 1 , e 2 . Приравнивая одноименные координаты векторов r и r 0 + t 1 e 1 + t 2 e 2 , получаем параметрические уравнения плоскости

Плоскость, проходящая через три точки. Предположим, что три точки M 1 , M 2 и М 3 не лежат на одной прямой. Тогда существует единственная плоскость π, которой эти точки принадлежат. Найдем уравнение этой плоскости, сформулировав критерий принадлежности произвольной точки M данной плоскости π. Затем запишем этот критерий через координаты точек. Указанным критерием является описание плоскости π как множества тех точек M, для которых векторы M 1 M 2 , M 1 M 3 и M 1 M компланарны . Критерием компланарности трех векторов является равенство нулю их смешанного произведения (см. 3.2). Смешанное произведение вычисляется с помощью определителя третьего порядка , строками которого являются координаты векторов в ортонормированном базисе . Поэтому, если (x i ; yx i ; Zx i) - координаты точек Mx i , i = 1, 2, 3, а (x; y; z) - координаты точки M, то M 1 M = {х-x 1 ; у-y 1 ; z-z 1 }, M 1 M 2 = {x 2 -x 1 ; y 2 -y 1 ; z 2 -z 1 }, M 1 M 3 = {x 3 -x 1 ; y 3 -y 1 ; z 3 -z 1 } и условие равенства нулю смешанного произведения этих векторов имеет вид
Вычислив определитель, получим линейное относительно x, y, z уравнение , являющееся общим уравнением искомой плоскости . Например, если разложить определитель по 1-й строке , то получим
Это равенство после вычисления определителей и раскрытия скобок преобразуется к общему уравнению плоскости.
Отметим, что коэффициенты при переменных в последнем уравнении совпадают с координатами векторного произведения M 1 M 2 × M 1 M 3 . Это векторное произведение, будучи произведением двух неколлинеарных векторов, параллельных плоскости π, дает ненулевой вектор, перпендикулярный π, т.е. ее нормальный вектор . Так что появление координат векторного произведения в качестве коэффициентов общего уравнения плоскости вполне закономерно.
Рассмотрим следующий частный случай плоскости, проходящей через три точки. Точки M 1 (a; 0; 0), M 2 (0; b; 0), M 3 (0; 0; c), abc ≠ 0, не лежат на одной прямой и задают плоскость, которая отсекает на осях координат отрезки ненулевой длины (рис. 5.3). Здесь под " длинами отрезков " понимают значение ненулевых координат радиус-векторов точек M i , i = 1,2,3.

Поскольку M 1 M 2 = {-a; b;0}, M 1 M 3 = {-a; 0; c}, M 1 M = (x-a; y; z), то уравнение (5.7) принимает вид

Вычислив определитель, найдем bc(x - a) + acy + abz = 0, разделим полученное уравнение на abc и перенесем свободный член в правую часть,
x/a + y/b + z/c = 1.
Это уравнение называют уравнением плоскости в отрезках .
Пример 5.2. Найдем общее уравнение плоскости, которая проходит через точку с координатами (1; 1; 2) и отсекает от осей координат отрезки одинаковой длины.
Уравнение плоскости в отрезках при условии, что она отсекает от осей координат отрезки равной длины, скажем a ≠ 0, имеет вид x/a + y/b + z/c = 1. Этому уравнению должны удовлетворять координаты (1; 1; 2) известной точки на плоскости, т.е. выполняется равенство 4/a = 1. Поэтому a = 4 и искомым уравнением является x + y + z - 4 = 0.
Нормальное уравнение плоскости. Рассмотрим некоторую плоскость π в пространстве. Фиксируем для нее единичный нормальный вектор n, направленный из начала координат "в сторону плоскости ", и обозначим через р расстояние от начала O системы координат до плоскости π (рис. 5.4). Если плоскость проходит через начало системы координат, то p = 0, а в качестве направления для нормального вектора n можно выбрать любое из двух возможных.
Если точка M принадлежит плоскости π, то это эквивалентно тому, что ортогональная проекция вектора OM на направление вектора n равна р, т.е. выполнено условие nOM = пр n OM = р, так как длина вектора n равна единице.
Обозначим координаты точки M через (x; y; z) и пусть n = {cosα; cosβ; cosγ} (напомним, что для единичного вектора n его направляющие косинусы cosα, cosβ, cosγ одновременно являются и его координатами). Записывая скалярное произведение в равенстве nOM = р в координатной форме, получаем нормальное уравнение плоскости
xcosα + ycosbeta; + zcosγ - p = 0.

Аналогично случаю прямой на плоскости, общее уравнение плоскости в пространстве можно преобразовать в ее нормальное уравнение делением на нормирующий множитель.
Для уравнения плоскости Ax + By + Cz + D = 0 нормирующим множителем является число ±√(A 2 + B 2 + C 2), знак которого выбирается противоположным знаку D. По абсолютной величине нормирующий множитель представляет собой длину нормального вектора {A; B; C} плоскости, а знак соответствует нужному направлению единичного нормального вектора плоскости. Если плоскость проходит через начало системы координат, т.е. D = 0, то знак нормирующего множителя можно выбрать любым.
До сих пор мы рассматривали уравнение поверхности в пространстве с координатными осями Х, Y, Z в явной форме или в неявной форме
![]()
Можно написать уравнения поверхности в параметрической форме, выражая координаты ее точек в виде функций двух независимых переменных параметров и
Мы будем предполагать, что эти функции однозначны, непрерывны и имеют непрерывные производные до второго порядка в некоторой области изменения параметров
Если подставить эти выражения координат через u и v в левую часть уравнения (37), то мы должны получить тождество относительно и и V. Дифференцируя это тождество по независимым переменным и и v, будем иметь

Рассматривая эти уравнения как два однородных уравнения относительно и применяя алгебраическую лемму, упомянутую в , получим

где k - некоторый коэффициент пропорциональности.
Мы считаем, что множитель к и по крайней мере одна из разностей, стоящих в правых частях последних формул, отличны от нуля.
Обозначим для краткости написанные три разности следующим образом:

Как известно, уравнение касательной плоскости к нашей поверхности в некоторой ее точке (х, у, z) можно написать в виде
или, заменяя пропорциональными величинами, можем переписать уравнение касательной плоскости так:
Коэффициенты в этом уравнении, как известно, пропорциональны направляющим косинусам нормали к поверхности.
Положение переменной точки М на поверхности характеризуется значениями параметров и и v, и эти параметры называются обычно координатами точек поверхности или координатными параметрами.
Придавая параметрам и и v постоянные значения, получим два семейства линий на поверхности, которые мы назовем координатными линиями поверхности: координатные линии вдоль которых меняется только v, и координатные линии вдоль которых меняется только и. Эти два семейства координатных линий дают координатную сетку на поверхности.
В качестве примера рассмотрим сферу с центром в начале координат и радиусом R. Параметрические уравнения такой сферы могут быть написаны в виде
Координатные, линии представляют собой в данном случае, очевидно, параллели и меридианы нашей сферы.
Отвлекаясь от координатных осей, мы можем охарактеризовать поверхность переменным радиусом-вектором идущим из постоянной точки О в переменную точку М нашей поверхности. Частные производные от этого радиуса-вектора по параметрам дадут, очевидно, векторы, направленные по касательным к координатным линиям. Составляющие этих векторов по осям
будут, согласно и отсюда видно, что коэффициенты в уравнении касательной плоскости (39) суть составляющие векторного произведения Это векторное произведение есть вектор, перпендикулярный к касательным т. е. вектор, направленный по нормали поверхности. Квадрат длины этого вектора выражается, очевидно, скалярным произведением вектора на самого себя, т. е. проще говоря, квадратом этого вектора 1). В дальнейшем будет играть существенную роль единичный вектор нормали к поверхности, который мы можем, очевидно, написать в виде

Изменяя порядок сомножителей в написанном векторном произведении, мы получим для вектора (40) противоположное направление. Мы будем в дальнейшем определенным образом фиксировать порядок множителей, т. е. будем определенным образом фиксировать направление нормали к поверхности.
Возьмем на поверхности некоторую точку М и проведем через эту точку какую-либо кривую (L), лежащую на поверхности. Эта кривая, вообще говоря, не координатная линия, и вдоль нее будут меняться как Ну так и v. Направление касательной к этой кривой будет определяться вектором если считать, что вдоль (L) в окрестности точки параметр v есть функция от имеющая производную. Отсюда видно, что направление касательной к кривой, проведенной на поверхности, в какой-либо точке М этой кривой, вполне характеризуется величиной в этой точке. При определении Касательной плоскости и выводе ее уравнения (39) мы считали, что функции (38) в рассматриваемой точке и ее окрестности имеют непрерывные частные производные и что, по крайней мере, один из коэффициентов уравнения (39) отличен от нуля в рассматриваемой точке.
– общее уравнение плоскости в пространстве
Нормальный вектор плоскости
Нормальным вектором плоскости назовем ненулевой вектор, ортогональный каждому вектору, лежащему в плоскости.
Уравнение плоскости, проходящей через точкус заданным вектором нормали
– уравнение плоскости, проходящей через точку M0 с заданным вектором нормали
Направляющие векторы плоскости
Два неколлинеарных вектора, параллельных плоскости, назовем направляющими векторами плоскости
Параметрические уравнения плоскости
![]() – параметрическое уравнение плоскости
в векторном виде
– параметрическое уравнение плоскости
в векторном виде
 – параметрическое уравнение плоскости
в координатах
– параметрическое уравнение плоскости
в координатах
Уравнение плоскости через заданную точку и два направляющих вектора
–фиксированная точка
–просто точка лол
–компланарные, значит их смешанное произведение равно 0.

Уравнение плоскости, проходящей через три заданные точки
 – уравнение плоскости через три точки
– уравнение плоскости через три точки
Уравнение плоскости в отрезках
– уравнение плоскости в отрезках
Доказательство
Для доказательства воспользуемся тем, что наша плоскость проходит через A,B,C, а нормальный вектор

Подставим координаты точки и вектораnв уравнение плоскости с нормальным вектором
Разделим все на и получим
Такие дела.
Нормальное уравнение плоскости
– угол междуoxи нормальным вектором к плоскости, выходящим из О.
– угол междуoyи нормальным вектором к плоскости, выходящим из О.
– угол междуozи нормальным вектором к плоскости, выходящим из О.
– расстояние от начала координат до плоскости.
Доказательство или какая-то такая хуйня
![]()
Знак противоположен D.
Аналогично для остальных косинусов. Конец.
Расстояние от точки до плоскости
Точка S, плоскость
– ориентированное расстояние от точкиSдо плоскости
Если , тоSи О лежат по разные стороны от плоскости
Если , тоSи О лежат по одну сторону
Умножаем наn
![]()
Взаимное расположение двух прямых в пространстве
Угол между плоскостями
При пересечении образуется две пары вертикальных двухгранных углов, наименьший называется углом между плоскостями
Прямая в пространстве
Прямая в пространстве может быть задана как
Пересечение двух плоскостей:
![]()
![]()
Параметрические уравнения прямой
– параметрическое уравнение прямой в векторном виде
– параметрическое уравнение прямой в координатах
Каноническое уравнение
![]() – каноническое уравнение прямой.
– каноническое уравнение прямой.
Уравнение прямой, проходящей через две заданные точки
![]()
![]() – каноническое уравнение прямой в
векторном виде;
– каноническое уравнение прямой в
векторном виде;
Взаимное расположение двух прямых в пространстве
Взаимное расположение прямой и плоскости в пространстве
Угол между прямой и плоскостью
Расстояние от точки до прямой в пространстве
a– направляющий вектор нашей прямой.
– произвольная точка, принадлежащая данной прямой
– точка, до которой ищем расстояние.
Расстояние между двумя скрещивающимися прямыми
Расстояние между двумя параллельными прямыми
М1 – точка, принадлежащая первой прямой
М2 – точка, принадлежащая второй прямой
![]()
Кривые и поверхности второго порядка
Эллипсом назовем множество точек плоскости, сумма расстояний от которых до двух заданных точек (фокусов) есть величина постоянная.
Каноническое уравнение эллипса



Заменим на
![]()
Разделим на
Свойства эллипса
Пересечение с осями координат
Начала координат
Симметрия относительно
Эллипс представляет собой кривую, лежащую в ограниченной части плоскости
Эллипс можно получить из окружности путем её растяжения или сжатия
Параметрическое уравнение эллипса:
– директрисы
Гипербола
Гиперболой назовем множество точек плоскости, для которых модуль разности расстояний до 2х заданных точек (фокусов) есть величина постоянная(2a)

Делаем все то же самое, что и с эллипсом, получаем
Заменяем на
Делим на
Свойства гиперболы
;
![]()
– директрисы
Асимптота
Асимптота – прямая, к которой кривая неограниченно приближается, удаляясь в бесконечность.
Парабола

Свойства паработы
Родство эллипса, гиперболы и параболы.
Родство между этими кривыми имеет алгебраическое объяснение: все они задаются уравнениями второй степени. В любой системе координат уравнения этих кривых имеют вид: ax 2 +bxy+cy 2 +dx+ey+f=0, где a, b, c, d, e, f – числа
Преобразование прямоугольных декартовых систем координат
Параллельный перенос системы координат
![]()
–O’ в старой системе координат
–координаты точки в старой системе координат
–координаты точки в новой системе координат
Координаты точки в новой системе координат.
Поворот в прямоугольной декартовой системе координат
–новая система координат
![]()
Матрица перехода от старого базиса к новому
![]() – (под первым столбцомI
’
,
под вторым –j
’
)
матрица перехода от базисаI
,j
к базисуI
’
,j
’
– (под первым столбцомI
’
,
под вторым –j
’
)
матрица перехода от базисаI
,j
к базисуI
’
,j
’
![]()
![]()
Общий случай
Поворот системы координат
Поворот системы координат
Параллельный перенос начала координат
1 вариант
2 вариант
Общее уравнение линий второго порядка и его приведение к каноническому виду
– общий вид уравнений кривой второго порядка
Классификация кривых второго порядка
Эллипсоид
![]()
Сечения эллипсоида
– эллипс
– эллипс
![]()
![]()
Эллипсоиды вращения
Эллипсоидами вращения являются либо сплющенные, либо вытянутые сфероиды, в зависимости от того, вокруг чего вращаем.
Однополосный гиперболоид
![]()

Сечения однополосного гиперболоида
– гипербола с действительной осьюoy
– гипербола с действительной осью ох
![]()
Получается эллипс при любых h. Такие дела.
Однополосные гиперболоиды вращения
Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси.
Двуполостный гиперболоид
![]()
Сечения двуполостного гиперболоида
– гипербола с действ. Осьюoz
– гипербола с действительной осьюoz
![]()
Конус
![]()
– пара пересекающихся прямых
– пара пересекающихся прямых
Эллиптический параболоид
![]() -
парабола
-
парабола
– парабола
Вращения
Если , то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг её оси симметрии.
Гиперболический параболоид

Парабола
– парабола
h>0 гипербола с действительной осью параллельной ох
h<0 гипербола с действительной осью паралльной оу и мнимой ох
Под цилиндром будем понимать поверхность, которая будет получаться при движении прямой в пространстве, не меняющая своего направления, если прямая движется относительно oz, то уравнение цилиндра есть уравнение сечения плоскостьюxoy.
Эллиптический цилиндр

Гиперболический цилиндр

Параболический цилиндр

Прямолинейные образующие поверхностей второго порядка
Прямые, полностью лежащие на поверхности, называются прямолинейными образующими поверхности.
![]()
![]()


Поверхности вращения
Ебать ты лох
Отображение
Отображением назовем правило, по которому каждому элементу множества А ставится в соответствие один или несколько элементов множестваB. Если каждому ставится единственный элемент множества В, то отображение называетсяоднозначным , иначемногозначным .
Преобразованием множества называется взаимнооднозначное отображение множества на себя
Инъекция
Инъекция или взаимно-однозначное отображение множества А на множество В
(разным элементам а соответствуют разные элементы В) например y=x^2

Сюръекция
Сюръекция или отображение множества А на множество В
Для каждого В существует хотя бы одно А(например синус)

Каждому элементу множества В соответствует только один элемент множества А.(например y=x)
Всякое уравнение первой степени относительно координат x, y, z
Ax + By + Cz +D = 0 (3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости .
Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)
2) двумя своими точками M 1 (x 1 , y 1 , z 1) и M 2 (x 2 , y 2 , z 2), тогда прямая, через них проходящая, задается уравнениями:
3) точкой M 1 (x 1 , y 1 , z 1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой .
Вектор a называется направляющим вектором прямой .
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x 1 + mt , y = y 1 + nt , z = z 1 + р t . (3.5)
Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y , приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой :
x = mz + a, y = nz + b. (3.6)
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n 1 , n 2 ], где n 1 (A 1 , B 1 , C 1) и n 2 (A 2 , B 2 , C 2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
равносильна системе ; такая прямая перпендикулярна к оси Ох.
Система равносильна системе x = x 1 , y = y 1 ; прямая параллельна оси Oz.
Пример 1.15 . Cоставьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение.
По условию задачи вектор ОА
(1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
x-y+3z+D=0. Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 1-(-1)+3 × 3+D = 0 Þ D = -11. Итак, x-y+3z-11=0.
Пример 1.16 . Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью 2x+y- z-7=0 угол 60 о.
Решение.
Плоскость, проходящая через ось Oz, задается уравнением Ax+By=0, где А и В одновременно не обращаются в нуль. Пусть В не
равно 0, A/Bx+y=0. По формуле косинуса угла между двумя плоскостями
Решая квадратное уравнение 3m 2 + 8m - 3 = 0, находим его корни
m 1 = 1/3, m 2 = -3, откуда получаем две плоскости 1/3x+y = 0 и -3x+y = 0.
Пример 1.17.
Составьте канонические уравнения прямой:
5x + y + z = 0, 2x + 3y - 2z + 5 = 0.
Решение. Канонические уравнения прямой имеют вид:
где m, n, р - координаты направляющего вектора прямой, x 1 , y 1 , z 1 - координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, x=0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть x=0, тогда y + z = 0, 3y - 2z+ 5 = 0, откуда y=-1, z=1. Координаты точки М(x 1 , y 1 , z 1), принадлежащей данной прямой, мы нашли: M (0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей n 1 (5,1,1) и n 2 (2,3,-2). Тогда
Канонические уравнения прямой имеют вид: x/(-5) = (y + 1)/12 =
= (z - 1)/13.