Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Деформация.
Силы упругости возникают при деформациях тел. Деформация
- это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация
полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация
сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости - это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример - сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Закон Гука.
Деформация называется малой , если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.
Закон Гука . Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:
(1)
где - коэффициент жёсткости пружины.
Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.
Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):
 |
| Рис. 1. Закон Гука |
Коэффициент жёсткости - о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:
где - угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .
Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 - это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .
Модуль Юнга.
В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.
Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать
на величину , то для силы упругости справедлива формула:
Здесь - модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.
Коэффициент E в этой формуле называется модулем Юнга . Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E ≈ 2·10 11 Н/м 2 , а для резины E ≈ 2·10 6 Н/м 2 , то есть на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры . При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления . Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела .
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины . В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром . Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
| Рисунок 1.12.3. Деформация растяжения пружины. |
В отличие от пружин и некоторых эластичных материалов (например, резины) деформация растяжения или сжатия упругих стержней (или проволок) подчиняется линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
§ 10. Сила упругости. Закон Гука
Виды деформаций
Деформацией
называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил.
Деформации, полностью исчезающие после прекращения действия на тело внешних сил, называют упругими
, а деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело, - пластическими
.
Различают деформации растяжения
или сжатия
(одностороннего или всестороннего), изгиба
, кручения
и сдвига
.
Силы упругости
При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.
Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела. Природа упругих сил электрическая.
Мы рассмотрим случай возникновения сил упругости при одностороннем растяжении и сжатии твердого тела.
Закон Гука
Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид
где f - сила упругости; х - удлинение (деформация) тела; k - коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ - ньютон на метр (Н/м).
Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.
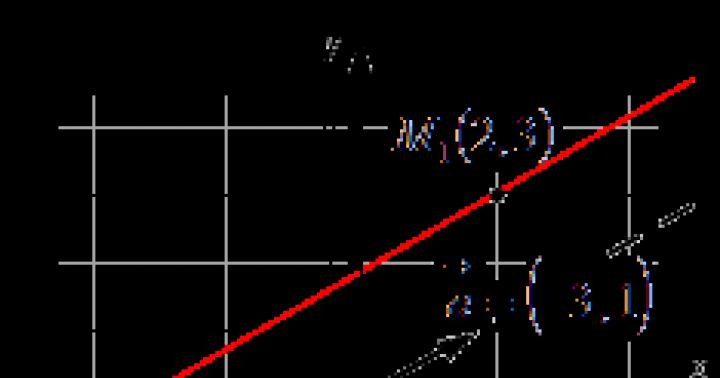
Рассмотрим опыт, иллюстрирующий закон Гука. Пусть ось симметрии цилиндрической пружины совпадает с прямой Ах (рис. 20, а). Один конец пружины закреплен в опоре в точке А, а второй свободен и к нему прикреплено тело М. Когда пружина не деформирована, ее свободный конец находится в точке С. Эту точку примет за начало отсчета координаты х, определяющей положение свободного конца пружины.
Растянем пружину так, чтобы ее свободный конец находился в точке D, координата которой х>0: В этой точке пружина действует на тело М упругой силой
Сожмем теперь пружину так, чтобы ее свободный конец находился в точке В, координата которой х<0. В этой точке пружина действует на тело М упругой силой
Из рисунка видно, что проекция силы упругости пружины на ось Ах всегда имеет знак, противоположный знаку координаты х, так как сила упругости направлена всегда к положению равновесия С. На рис. 20, б изображен график закона Гука. На оси абсцисс откладывают значения удлинения х пружины, а на оси ординат - значения силы упругости. Зависимость fх от х линейная, поэтому график представляет собой прямую, проходящую через начало координат.
Рассмотрим еще один опыт.
Пусть один конец тонкой стальной проволоки закреплен на кронштейне, а к другому концу подвешен груз, вес которого является внешней растягивающей силой F, действующей на проволоку перпендикулярно ее поперечному сечению (рис. 21).
Действие этой силы на проволоку зависит не только от модуля силы F, но и от площади поперечного сечения проволоки S.
Под действием приложенной к ней внешней силы проволока деформируется, растягивается. При не слишком большом растяжении эта деформация является упругой. В упруго деформированной проволоке возникает сила упругости f уп.
Согласно третьему закону Ньютона, сила упругости равна по модулю и противоположна по направлению внешней силе, действующей на тело, т. е.
f уп = -F (2.10)
Состояние упруго деформированного тела характеризуют величиной s, называемой нормальным механическим напряжением (или, для краткости, просто нормальным напряжением ). Нормальное напряжение s равно отношению модуля силы упругости к площади поперечного сечения тела:
s=f уп /S (2.11)
Пусть первоначальная длина нерастянутой проволоки составляла L 0 . После приложения силы F проволока растянулась и ее длина стала равной L. Величину DL=L-L 0 называют абсолютным удлинением проволоки . Величину
называют относительным удлинением тела . Для деформации растяжения e>0, для деформации сжатия e<0.
Наблюдения показывают, что при небольших деформациях нормальное напряжение s пропорционально относительному удлинению e:
Формула (2.13) является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным. Коэффициент пропорциональности Е в законе Гука называется модулем продольной упругости (модулем Юнга).
Установим физический смысл модуля Юнга. Как видно из формулы (2.12), e=1 и L=2L 0 при DL=L 0 . Из формулы (2.13) следует, что в этом случае s=Е. Следовательно, модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза. (если бы для такой большой деформации выполнялся закон Гука). Из формулы (2.13) видно также, что в СИ модуль Юнга выражают в паскалях (1 Па = 1 Н/м 2).
Диаграмма растяжения
Используя формулу (2.13), по экспериментальным значениям относительного удлинения e можно вычислить соответствующие им значения нормального напряжения s, возникающего в деформированном теле, и построить график зависимости s от e. Этот график называют диаграммой растяжения . Подобный график для металлического образца изображен на рис. 22. На участке 0-1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, т. е. нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения s п, при котором еще выполняется закон Гука, называют пределом пропорциональности .
При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1-2), хотя упругие свойства тела еще сохраняются. Максимальное значение s у нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости . (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2-3) приводит к тому, что деформация становится остаточной.
Затем образец начинает удлиняться практически при постоянном напряжении (участок 3-4 графика). Это явление называют текучестью материала. Нормальное напряжение s т, при котором остаточная деформация достигает заданного значения, называют пределом текучести .
При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4-5 графика). Максимальное значение нормального напряжения s пр, при превышении которого происходит разрыв образца, называют пределом прочности .
Энергия упруго деформированного тела
Подставив в формулу (2.13) значения s и e из формул (2.11) и (2.12), получим
f уп /S=E|DL|/L 0 .
откуда следует, что сила упругости f уп, возникающая при деформации тела, определяется по формуле
f уп =ES|DL|/L 0 . (2.14)
Определим работу A деф, совершаемую при деформации тела, и потенциальную энергию W упруго деформированного тела. Согласно закону сохранения энергии,
W=A деф. (2.15)
Как видно из формулы (2.14), модуль силы упругости может изменяться. Он возрастает пропорционально деформации тела. Поэтому для подсчета работы деформации необходимо брать среднее значение силы упругости
Тогда определяемая по формуле A деф =
A деф = ES|DL| 2 /2L 0 .
Подставив это выражение в формулу (2.15), найдем значение потенциальной энергии упруго деформированного тела:
W= ES|DL| 2 /2L 0 . (2.17)
Для упруго деформированной пружины ES/L 0 =k - жесткость пружины; х - удлинение пружины. Поэтому формула (2.17) может быть записана в виде
W=kx 2 /2. (2.18)
Формула (2.18) определяет потенциальную энергию упруго деформированной пружины.
Вопросы для самоконтроля:
Что такое деформация?
Какую деформацию называют упругой? пластической?
Назовите виды деформаций.
Что такое сила упругости? Как она направлена? Какова природа этой силы?
Как формулируется и записывается закон Гука для одностороннего растяжения (сжатия)?
Что такое жесткость? Какова единица жесткости в СИ?
Начертите схему и объясните опыт, иллюстрирующий закон Гука. Постройте график этого закона.
Сделав пояснительный рисунок, опишите процесс растяжения металлической проволоки под нагрузкой.
Что называют нормальным механическим напряжением? Какая формула выражает смысл этого понятия?
Что называют абсолютным удлинением? относительным удлинением? Какие формулы выражают смыйл этих понятий?
Какой вид имеет закон Гука в записи, содержащей нормальное механическое напряжение?
Что называют модулем Юнга? Каков его физический смысл? Какова единица модуля Юнга в СИ?
Начертите и объясните диаграмму растяжения металлического образца.
Что называют пределом пропорциональности? упругости? текучести? прочности?
Получите формулы, по которым определяют работу деформации и потенциальную энергию упруго деформированного тела.
Многие ли из нас задумывались, каким удивительным образом ведут себя предметы при воздействии на них?
Например, почему ткань, если мы растягиваем ее в разные стороны, может долго тянуться, а в один момент вдруг порваться? И почему тот же самый эксперимент куда сложнее провести с карандашом? От чего зависит сопротивление материала? Каким образом можно определить, до какой степени он поддается деформации или растяжению?
Все эти и многие другие вопросы более 300 лет назад задавал себе английский исследователь И нашел ответы, ныне объединенные под общим названием "Закон Гука".
Согласно его исследованиям, каждый материал имеет так называемый коэффициент упругости . Это свойство, позволяющее материалу растягиваться в определенных пределах. Коэффициент упругости - величина постоянная. Это значит, что каждый материал может выдержать лишь определенный уровень сопротивления, после чего он достигает уровня необратимой деформации.
В целом, Закон Гука можно выразить формулой:
где F - сила упругости, k - уже упомянутый коэффициент упругости, а /x/ - изменение длины материала. Что подразумевается под изменением этого показателя? Под воздействием силы некий изучаемый предмет, будь это струна, резина или любой другой, изменяются, вытягиваясь или сжимаясь. Изменением длины в данном случае считается разница между изначальной и конечной длиной изучаемого предмета. То есть то, на сколько вытянулась/сжалась пружина (резина, струна и т.д.)
Отсюда, зная длину и постоянный коэффициент упругости для данного материала, можно найти силу, с которой материал натягивается, или силу упругости, как еще нередко называют Закон Гука.
Существуют также особые случаи, при которых данный закон в своей стандартной форме использован быть не может. Речь идет об измерении силы деформации в условиях сдвига, то есть в ситуациях, когда деформацию производит некая сила, воздействующая на материал под углом. Закон Гука при сдвиге может быть выражен таким образом:
где τ - искомая сила, G- постоянный коэффициент, известный как модуль упругости при сдвиге, y - угол сдвига, та величина, на которую изменился угол наклона предмета.
Если на тело воздействовать некоторой силой, то его размер и (или) форма изменяются. Это процесс называют деформацией тела. В телах, подвергающихся деформациям, возникают силы упругости, уравновешивающие внешние силы.
Виды деформации
Все деформации можно разделить на два вида: упругие деформации и пластические .
Определение
Упругой называют деформацию, если после снятия нагрузки прежние размеры тела и его форма полностью восстанавливаются.
Определение
Пластической считают деформацию, при которой появившиеся, вследствие деформации, изменения размера и формы тела, после снятия нагрузки восстанавливаются частично.
Характер деформации зависит от
- величины и времени воздействия внешней нагрузки;
- материала тела;
- состояния тела (температуры, способов обработки и т.д).
Резкой границы между упругой и пластической деформациями не существует. В большом числе случаев малые и кратковременные деформации можно считать упругими.
Формулировки закона Гука
Эмпирически получено, что чем большую деформацию необходимо получить, тем большую деформирующую силу следует приложить к телу. По величине деформации ($\Delta l$) можно судить о величине силы:
\[\Delta l=\frac{F}{k}\left(1\right),\]
выражение (1) означает, что абсолютная величина упругой деформации прямо пропорциональная приложенной силе. Данное утверждение является содержанием закона Гука.
При деформации удлинения (сжатия) тела выполняется равенство:
где $F$ - деформирующая сила; $l_0$ - начальная длина тела; $l$ - длина тела после деформации; $k$ - коэффициент упругости (коэффициент жесткости, жесткость), $ \left=\frac{Н}{м}$. Коэффициент упругости зависит от материала тела, его размеров и формы.
Так как в деформированном теле возникают силы упругости ($F_u$), которые стремятся восстановить прежние размеры и форму телу, то часто закон Гука формулируют относительно сил упругости:
Закон Гука хорошо работает для деформаций, которые возникают в стержнях из стали, чугуна, и других твердых веществ, в пружинах. Справедлив закон Гука для деформаций растяжения и сжатия.
Закон Гука для малых деформаций
Сила упругости зависит от изменения расстояния между частями одного и того же тела. Следует помнить, что закон Гука выполняется только для малых деформаций. При больших деформациях сила упругости не пропорциональна измерению длины, при дальнейшем увеличении деформирующего воздействия тело способно разрушаться.
Если деформации тела малы, то силы упругости можно определять по ускорению, которое данные силы сообщают телам. Если тело неподвижно, то модуль силы упругости находят из равенства нулю векторной суммы сил, которые действуют на тело.
Закон Гука можно записывать не только относительно сил, но часто его формулируют для такой величины как напряжение ($\sigma =\frac{F}{S}$ - сила, которая действует на единичную площадь поперечного сечения тела), тогда для малых деформаций:
\[\sigma =Е\frac{\Delta l}{l}\ \left(4\right),\]
где $Е$ - модуль Юнга;$\ \frac{\Delta l}{l}$ - относительное удлинение тела.
Примеры задач с решением
Пример 1
Задание. К стальному тросу длинной $l$, диаметром $d$ подвесили груз массой $m$. Каково напряжение в тросе ($\sigma $), а также абсолютное его удлинение ($\Delta l$)?
Решение. Сделаем рисунок.
Для того чтобы найти силу упругости, рассмотрим силы, которые действуют на тело, подвешенное к тросу, так как сила упругости будет равна по величине силе натяжения ($\overline{N}$). По второму закону Ньютона имеем:
В проекции на ось Y уравнения (1.1) получим:
По третьему закону Ньютона тело, действует на трос с силой равной по величине силе $\overline{N}$, трос, действует на тело с силой $\overline{F}$, равной$\overline{\ N,}$ но противоположного направления, так деформирующая трос сила ($\overline{F}$) равна:
\[\overline{F}=-\overline{N\ }\left(1.3\right).\]
Под воздействием деформирующей силы в тросе возникает сила упругости, которая равна по величине:
Напряжение в тросе ($\sigma $) найдем как:
\[\sigma =\frac{F_u}{S}=\frac{mg}{S}\left(1.5\right).\]
Площадь S - это площадь поперечного сечения троса:
\[\sigma =\frac{4mg\ }{{\pi d}^2}\left(1.7\right).\]
По закону Гука:
\[\sigma =Е\frac{\Delta l}{l}\left(1.8\right),\]
\[\frac{\Delta l}{l}=\frac{\sigma }{E}\to \Delta l=\frac{\sigma l}{E}\to \Delta l=\frac{4mgl\ }{{\pi d}^2E}.\]
Ответ. $\sigma =\frac{4mg\ }{{\pi d}^2};\ \Delta l=\frac{4mgl\ }{{\pi d}^2E}$
Пример 2
Задание. Какова абсолютная деформация первой пружины из двух последовательно соединенных пружин (рис.2), если коэффициенты жесткости пружин равны: $k_1\ и\ k_2$, а удлинение второй пружины составляет $\Delta x_2$?

Решение. Если система из последовательно соединенных пружин находится в состоянии равновесия, то силы натяжения данных пружин одинаковы:
По закону Гука:
Согласно (2.1) и (2.2) имеем:
Выразим из (2.3) удлинение первой пружины:
\[\Delta x_1=\frac{k_2\Delta x_2}{k_1}.\]
Ответ. $\Delta x_1=\frac{k_2\Delta x_2}{k_1}$.
Закон пропорциональности удлинения пружины приложенной силе был открыт английским физиком Робертом Гуком (1635-1703г.)
Научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными (Гюйгенс, Ньютоном и др.). Однако закон Гука был настолько убедительно обоснован многочисленными периментами, что тут приоритет Гука никогда не оспаривался.
Теория пружины Роберта Гука:
В этом и состоит закон Гука!
РЕШЕНИЕ ЗАДАЧ
Определить жесткость пружины, которая под действием силы 10 Н удлинилась на 5 см.
Дано:
g = 10 H/кг
F = 10H
X = 5см = 0,05м
Найти:
k = ?

Груз находится в равновесии.

Ответ: жесткость пружины k = 200H/м.
ЗАДАЧА НА "5"
(сдаем на листочке).
Объясните, почему безопасен прыжок акробата на сетку батута с большой высоты? (призываем на помощь Роберта Гука)
С нетерпением жду ответа!
МАЛЕНЬКИЙ ОПЫТ
Поставьте вертикально резиновую трубку, на которую предварительно туго надето металлическое кольцо, и растяните трубку. Что при этом произойдет с кольцом?
Динамика - Класс!ная физика